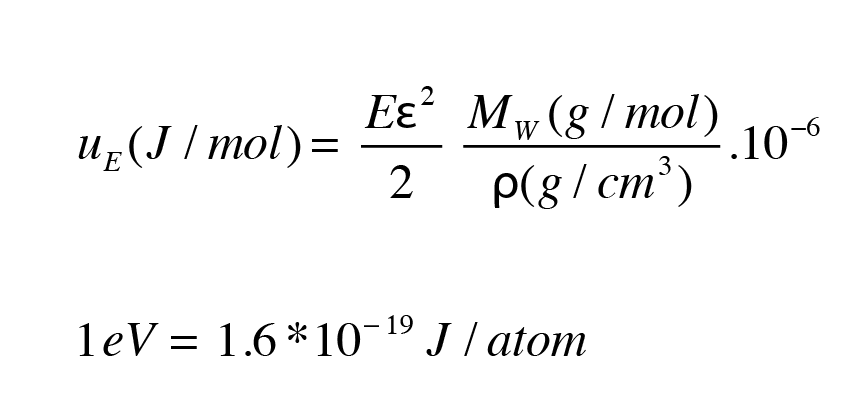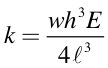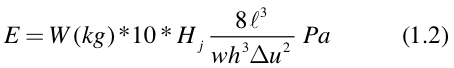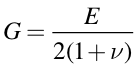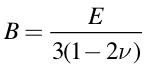Practice HW problems
The following excel file contains useful results and information. It will continue to be updated.
Here is the excel file
Problem 1.1
On a clean piece of paper derive the following equation, with a one line explanataion for each step in your analysis.
Equation 1.1
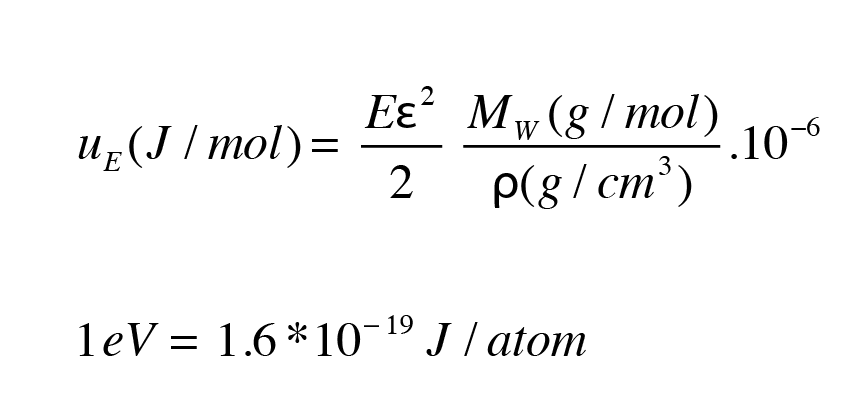
Now convert Eq. (1.1) into eV/atom. Calculate its value for copper at an elastic strain of 1%.
Problem 1.2
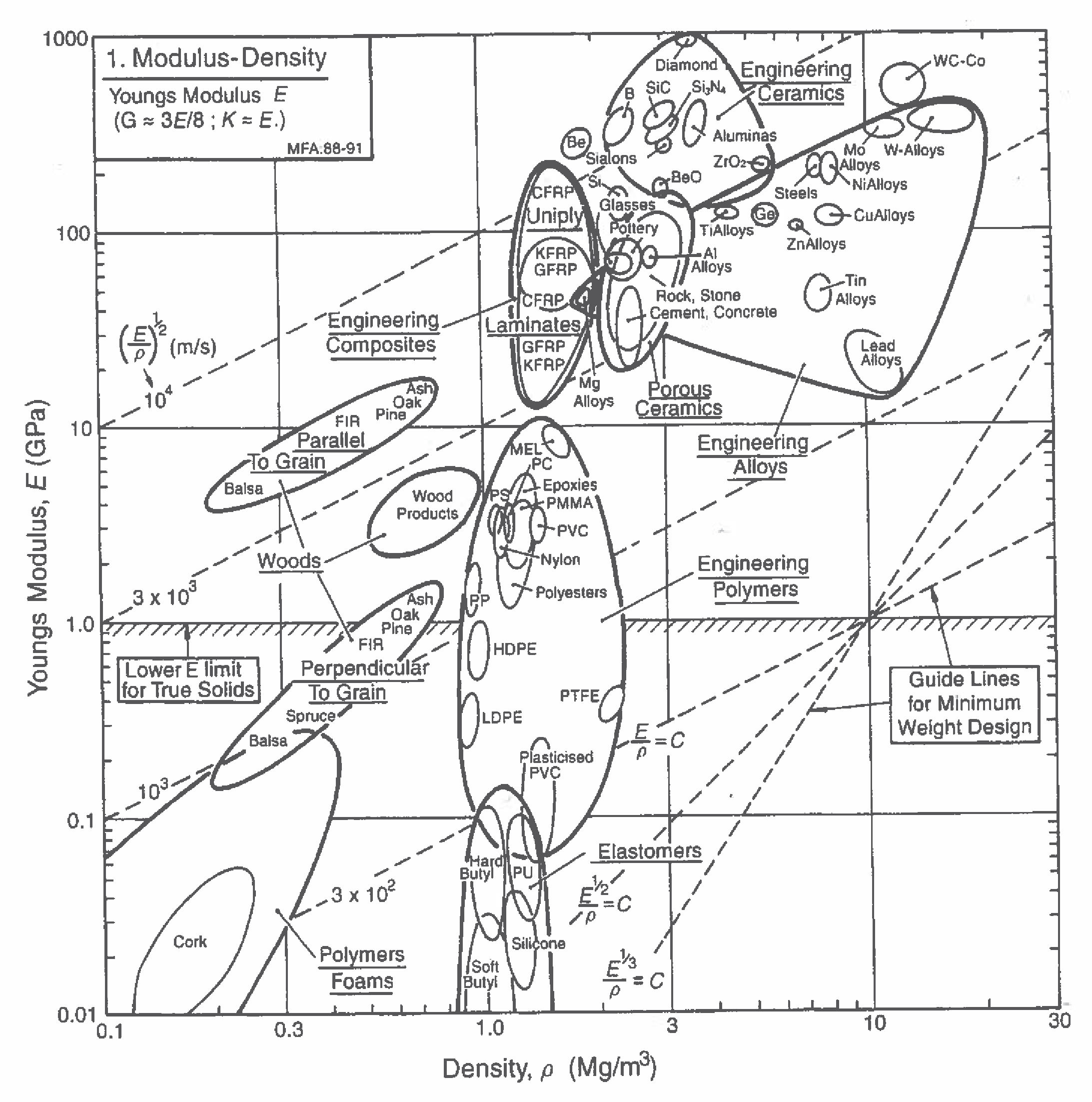
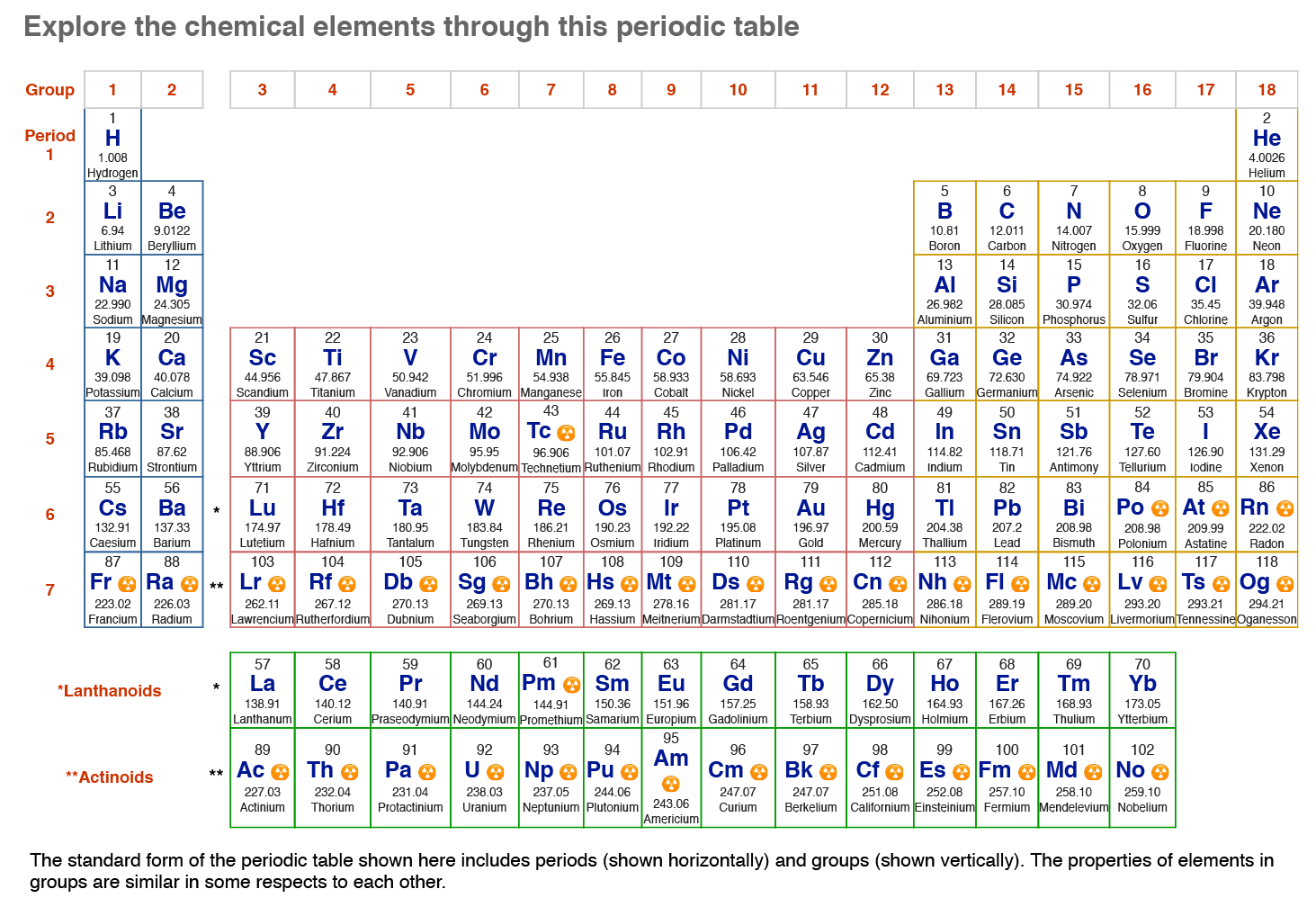
Use Eq. (1) to calculate the energy (in ev) per atom/molecule for (i) zirconium oxide, (ii) copper, (iii) tungsten, (iv) aluminum and (v) titanium oxide. You would need to look up the Youngs modulus and the density for these materials. Assume the elastic strain to be 20%.
Now look up the enthalpy of formation (or evaporation) for them also in eV
Make a plot of the enthalpy against the elastic energy to check to what extent they are related to one anothger.
Think about how the plot would change if you used an elastic strain of 10% instead of 20%.
Problem 1.3
In this problem you are asked to design a cantilever beam for (i) an atomic force microscope which can measure the stiffness of a DNA moledule, as shown below
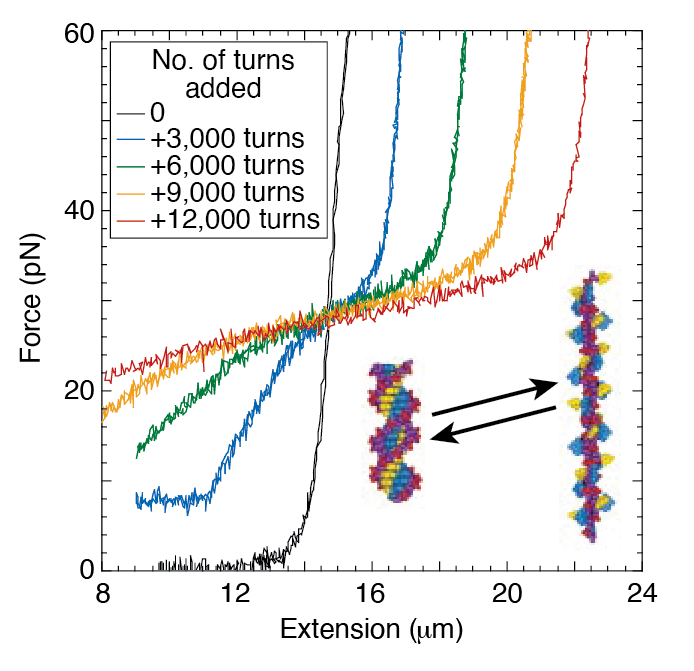
(ii) materials selecton for a diving board. Please refer to the .xlsx file give above.
The bending stiffness of a cantilever beam is given by the following equation. Here k, the stiffness is equal to the load at the tip of hte beam divided by its displacement, el is the length of the beam, w is its width and h its thickness. E is the Youngs Modulus. Note that k has units of N/m (please check)
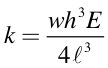
(a) Design a beam with silicon (E = 150 GPa) which will have a stiffness in the range of the DNA moledule
(b) Choose a material for a diving board where a person weighing 80 kg gets a lift of H_j (up in the air) from the beam bent to a displacement of u. Try to derive the following equation which is based upon the stored elastic energy in the beam that will be enough to lift the person up to a distance of H_j:
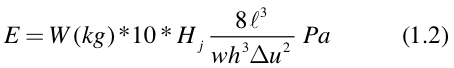
Problem 1.4
lease provide short written/verbal answers to the following questions
(i) Covalent bonds are nearly always stronger than metallic bonds?
(ii) Bonds arising from localized "electron cloud" overlap are stronger than those where the electron sharing is spread over several atom spaces?
(iii) Give examples of bonding with oxygen atoms (which likes to form two covalent bonds) which results in either a solid or a gas?
(iv) Why is ice a "weak solid" even though the bonds in the H2O molecule covalent?
(iv) Why is ice a "weak solid" even though the bonds in the H2O molecule covalent?
Problem 1.5
Write a descripion of principle axes, principal stresses and principal strains addressing the following points, (i) how they are defined, and (ii) give examples of how the principle axes can be sketched by inspection.
Problem 1.6
Give and example for pure shear deformation and pure volumetric deformation. Explain your answer with sketches and descriptions of the stress tensor
Problem 1.7
Give the srain tensors for the two situations given in Problem 1.6
Problem 1.8
Write down the stress and the strain tensor for uniaxial deformation. Then derive expressions for the volumetric and sheear deformation in a uniaxial test
Problem 1.9
Derive the following relationship between the Youngs Modulus and the Shear Modulus:
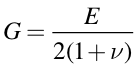
Write down the principle stresses and principal strains for (i) a uniaxial tension experiment, and (ii) a pure shear experiment. Be careful to show the principle axes in a sketch for both cases
Problem 1.10
Derive the following relationship between the Youngs Modulus and the Bulk Modulus:
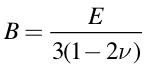
Problem 1.11
This problem pertains to the stresses that develop around a spherical includion where
(i) The elastic constants for the inclusion are different that those for the matrxi within which is it embedded, and
(ii) Stresses are created within the inclusion and in the matrix because they have different thermal expansion, when the temperature changes
The general equations for the stresses in a matrix with a spherical inhomogneity are given Equations for Spherical Incusion
These notes give the application of the equations to the case where the includion is rigid, that is, it has infinite stiffness
Now obtain the equations for the stresses in the inclusion and in the matrix when the inclusion has finite modulus which is different from that of the matrix, when the temaperature is changed by delat(T). The difference in the thermal expansion coefficient is delta(alpha)
Take Home Exam on Elastic Deformation of Solids and Solutions in Brief
Handed out 02/19, due on 02/26 during clas
Here are very brief answers to the questions in the homework exam